The Formula
k=\frac {\log(T_2)-\log(T_1)} {\log(I_1) - \log(I_2)}From the battery datasheet take two points and enter the Time and current draw into T1I1 and T2I2. The calculator will show the Peukert exponent based on the formula.
How accurate is it?
Well, the answer is, it depends. Batteries work on chemical reactions and will never follow Peukert’s Law perfectly, and the test points will have some margin of error in them.
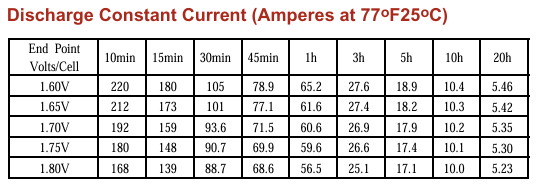
The above is data taken from a 100Ah 10hour battery. If you enter the data for1.75V end point 20hrs (5.30A) and 10hours (10.1A) the calculator gives 1.07 which is close to perfect. This is to be expected since the battery is rated at C10 and so C20 the capacity will be higher.
So, if we use the C10 point as T1 I1, and then calculate for T=1hr, we get 1.30, and 10 minutes 1.42
The point is – it varies, so what you really need to do is calculate based upon the expected level of discharge you will be experiencing, or take several results and average them.
However, if you want to get more accurate then we can take the data, take logs of each data set and graph it:
| Current | Time to 10.5V | log(I) | log(T) |
| 180 | 0.1667 | 5.192956851 | -1.791559489 |
| 148 | 0.25 | 4.997212274 | -1.386294361 |
| 90.7 | 0.5 | 4.507557357 | -0.6931471806 |
| 69.9 | 0.75 | 4.247065649 | -0.2876820725 |
| 59.6 | 1 | 4.087655574 | 0 |
| 26.6 | 3 | 3.280911216 | 1.098612289 |
| 17.4 | 5 | 2.856470206 | 1.609437912 |
| 10.1 | 10 | 2.312535424 | 2.302585093 |
| 5.3 | 20 | 1.667706821 | 2.995732274 |
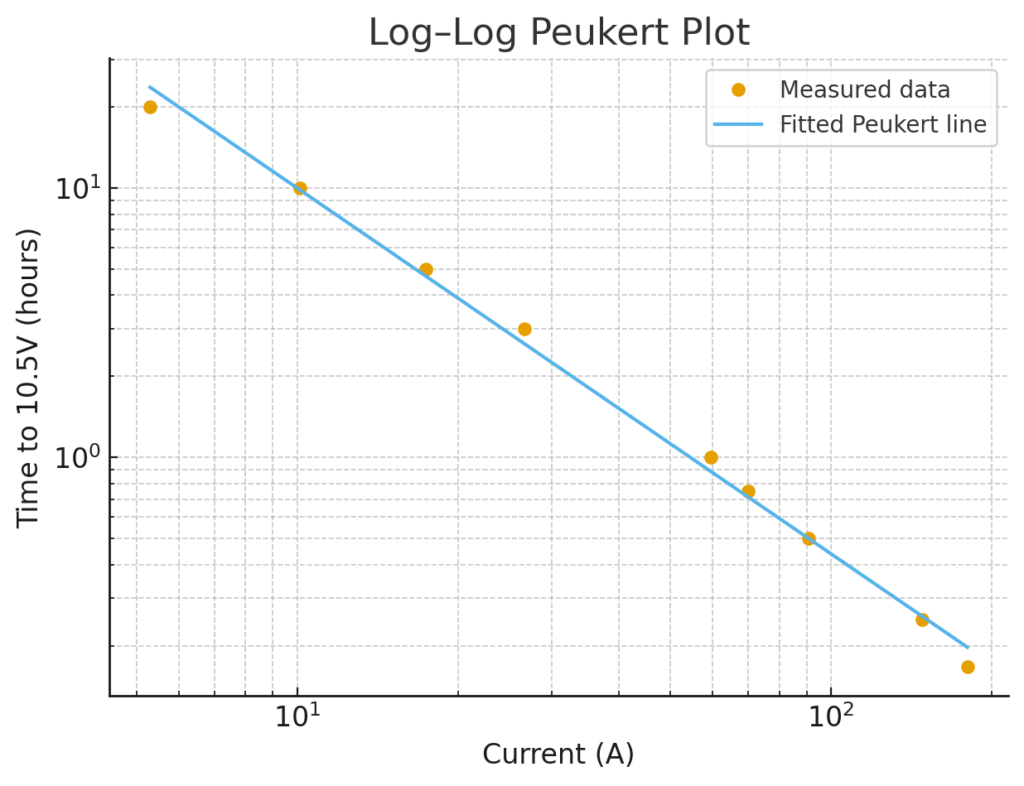
The gradient is the negative Peukert exponent (e.g. -k) and the value, in this case is 1.36